The word Cycloid, with its adjective Cycloidal, is derived from Hypocycloid which describes the curve traced by a point on the circumference of a smaller circle rotating inside the circumference of a larger fixed circle.  Just like words such as helical, worm, spur, and bevel, cycloidal is a generic adjective; it merely describes the gearing mechanism inside the speed reducer.  No manufacturers shall claim the exclusive use of this word.

To understand the operating principle, you should first know how to determine the reduction ratio of a cycloidal reducer.

Ratio = (P-L) / L

Where  P = Number of ring gear pins/rollers
            L = Number of lobes on a cycloidal disc

For example, please refer to drawing on the right, the number of ring gear pins/rollers (P) equals 12, and the number of lobes (L) on the cycloidal disc equals 11. 

Ratio = (12-11) / 11 = 1 / 11 = 11:1

- As the input shaft turns, the eccentric bearing goes into a rocking motion.  This rocking motion exerts an outward radial force on the cycloidal disc (Figure 1).

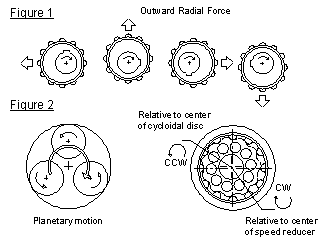
Confined inside the ring gear housing with pins/rollers, the cycloidal disc goes into a planetary motion as the eccentric bearing turns.  Refer to Figure 2, as a smaller circle rotates inside the circumference of a larger circle, the smaller circle goes into a planetary motion.  Relative to its own center, the smaller circle is rotating in the CCW direction.  However, relative to the center of larger circle, the smaller circle is advancing in the CW direction. (Figure 2, left)  Cycloidal mechanism works the same way.  The smaller circle as described earlier is now almost as large as the larger circle and has the shape of a cycloidal disc.  The larger circle now has the shape of a ring gear with pins/rollers. (Figure 2, right)  As the eccentric bearing drives the cycloidal disc, the cycloidal disc rotates in one direction relative to its own center.  However the cycloidal disc advances in the opposite direction relative to the center of the speed reducer.  This planetary motion looks almost like the wobbling movement of hula hoops.